上篇我們學習了抽象的數學理論，「環理論」（Ring Theory）。今天我們簡單複習模乘法的乘法反元素，用Sage實作。然後再討論「一個簡單二維晶格密碼系統」

什麼是乘法反元素？

假設我們在模除 m 的環中，考慮某個數字 a ，如果我們能找到另一個數字 b 而且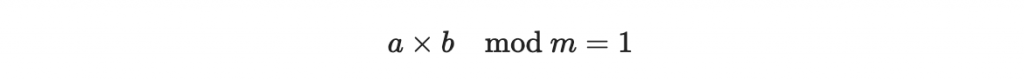

那我們會說 b 是 a 的乘法反元素，也可以記作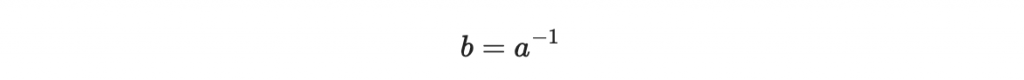

好我們可以馬上舉例子：

所以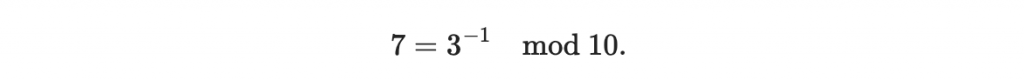

乘法反元素求法

首先，我們在模除 m 的環中，考慮某個數字 a ，當 a 與 m 的最大公因數等於一時， a 的反元素才會存在，反之亦然。

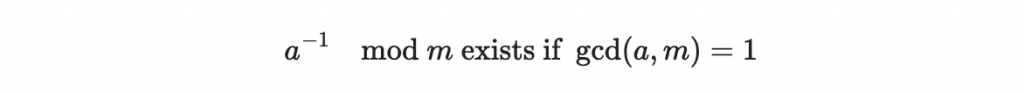
至於如何求到 a 的乘法反元素呢？實作上有兩大主流方法

• 擴展歐幾里德演算法（輾轉相除法）
• 費馬小定理

可是！因為我們有 SageMath ，所以我們不用那麼麻煩！

用 SageMath 來尋找反元素

主流的乘法反元素求法是歐幾里德演算法，那難道我們每次做密碼學實驗時，還得把歐幾里德演算法拿出來大算一波嗎？或是我每次在 python 做實驗時，都要重寫（或複製貼上我都嫌煩）一個歐幾里德演算法？

現在，我們來看看如何在 SageMath 中找到乘法反元素。只要幾行程式碼就可以解決：

# 在模 13 的情況下，找到 3 的乘法反元素
m = 13
R = quotient(ZZ, m*ZZ)
a = R(3) # a 是在 Ring of integers modulo 13 中的元素
b = a^(-1)  # 求反元素
print(b, type(b))  # 應該輸出 9, 以及反元素所在的類別

Outputs: 9 <class 'sage.rings.finite_rings.integer_mod.IntegerMod_int'>

一個簡單的二維晶格密碼系統？！

我們先放一張表在這裡，然後就一邊講一邊用SageMath做

（表格來源：我）

密碼系統說明

首先我們先確定目標：
Bob 想傳訊息給 Alice ， Alice 於是生成公私鑰，並給Bob公鑰來讓他加密送過來。

密鑰生成

Alice:
1, 選擇一個整數 q 作為模數
並且選擇兩個整數 f 以及 g
這些數字需要滿足以下條件：

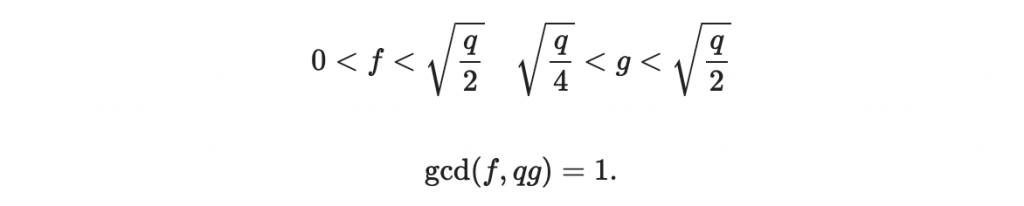
其中第二條的條件確保了以下兩個反元素的存在：

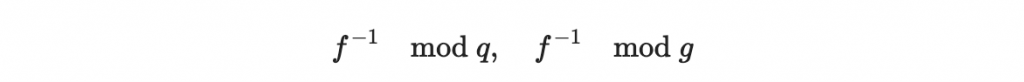
分別是整數 f 在模除 q 與模除 g 下的乘法反元素。模除 g 的反元素可以先算起來備用，也可以等等算，我們選擇後者。

# 生成需要的數字

while True:
    q = randint(1,(2**32)-1) 
    # 隨機生成一個介於 1 與 (2**32)-1 的整數
    
    f = randint(1, int(sqrt(q/2)))
    g = randint(int(sqrt(q/4)), int(sqrt(q/2)))
    if gcd(f, q*g)==1:
        break
print(q,f,g)

Outputs: 1408922792 1473 21881

2, 計算

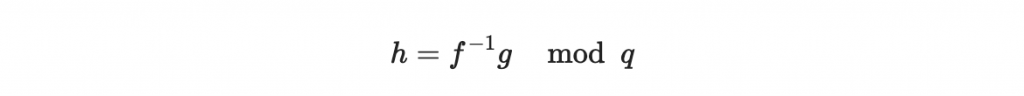
# 進行模運算

R_q = quotient(ZZ, q*ZZ);
f = R_q(f)
g = R_q(g)

h = f^(-1) * g
print(h)

Outputs: 466771449

3, 公佈公鑰：(q,h)
私鑰為：(f,g)

pk = (q,h) # 公鑰
sk = (f,g) # 私鑰
print(pk,sk)

Outputs: (1408922792, 466771449) (1473, 21881)

加密訊息

4, Bob先選擇要傳送的訊息 $m$ 以及一個隨機的 $r$ ，其中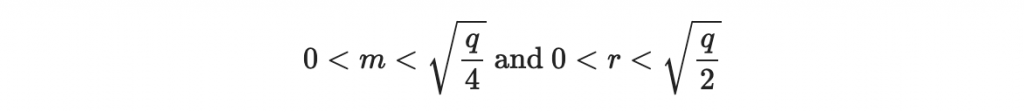

因為條件裡面有 q ，所以應該要等到拿到公鑰 (q, h) 後才開始做這步。

# Bob 加密訊息

m = randint(1, int(sqrt(q/4))) 
# 反正我也不是 Bob ，我就隨機幫他選一個訊息
r = randint(1, int(sqrt(q/2)))
print("the message is", m)

Outputs: the message is 15819

5, 計算密文為

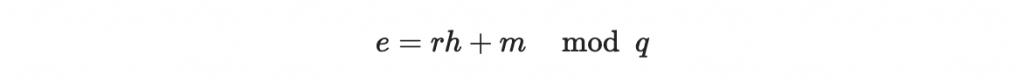
一樣因為算式裡面有 h 所以等到拿到公鑰後才能算

# 進行模運算
r = R_q(r)
m = R_q(m)
e = r*h + m
print(e)

Outputs: 1080936575

6, 傳送密文 e

解密訊息

7, Alice 拿到密文 e 後，做以下計算就可以得出訊息 $m$ ：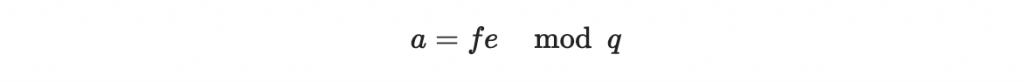

然後將 a 提升（lift）到原本的整數
（意思是，本來 a 是一個模除 q 的環裡面的元素，現在直接把它當作一個整數看、直接當成一個沒有模除過的整數環的元素）

# Alice 解密訊息
# 計算部分

a = f*e
print(a)

Outputs: 136820015

# (lift) 提升部分

print(a,type(a))
a = a.lift() # 提升
print(a,type(a))

Outputs:
136820015 <class 'sage.rings.finite_rings.integer_mod.IntegerMod_int64'>
136820015 <class 'sage.rings.integer.Integer'>

並再做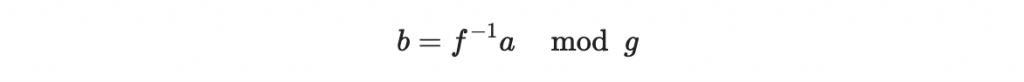

其中 b = m。

R_g = quotient(ZZ, g*ZZ)

a = R_g(a)
f = R_g(f.lift())
b = f^(-1) * a

print("b = ", b)
print("m = ", m)

Outputs:
b =  15819
m =  15819

到這裡你可能覺得，蛤？這樣可以解回 m ？我們等等就來證明

一個SageMath裡面的細節：

print(b == m)
print(type(b), type(m))

b = b.lift()
m = m.lift()

print(b == m)

Outputs: 
False
<class 'sage.rings.finite_rings.integer_mod.IntegerMod_int'> <class 'sage.rings.finite_rings.integer_mod.IntegerMod_int64'>
True

可以看到，因為我們的 m 與 b 定義在不同的類別，所以雖然數字一樣，使用相等運算子時可能會被判斷為錯誤，但你只要把他們都提升到整數環，兩個就一樣了～

正確性證明

（該來的還是要來）

首先我們看到，根據我們的構造，我們有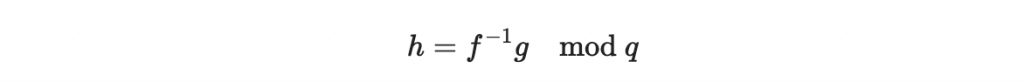

因此，「在模除 q 的環中」，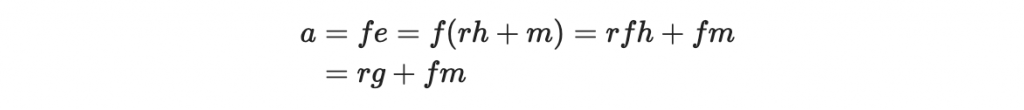

又根據我們對 r, g, f, m 的條件：

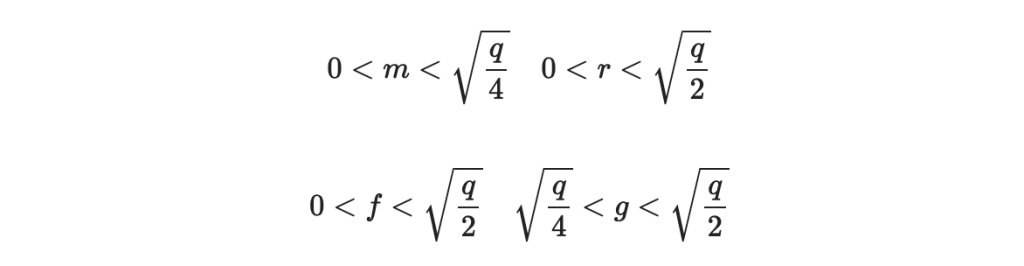
我們於是知道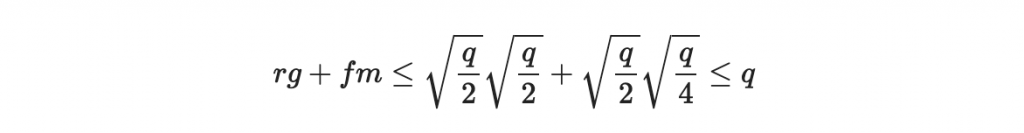

也就是說，rg+fm 這個數字，從構造條件上就確保了他不會超過q，因此，Alice根據我們密碼系統所算出來的 a = fe ，完完全全等於 rg+fm。

請注意一個決定性的差別：上面提到「在模除 q 的環中」，

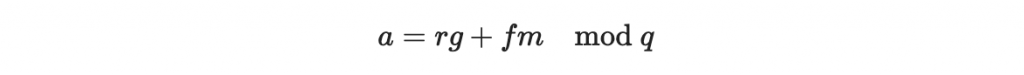
這裡的等號是指說，從整數的觀點看，數字 a 與 rg+fm 差了整數倍的 q。

而因為 rg + fm 根本就不會超過 q ，所以我們確保 a 與 rg+fm 在整數上根本完完全全相等。『並不是差了整數倍的 q ，而是完完全全的相等』

此時，我們就可以寫下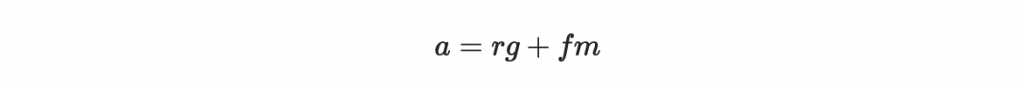

現在將這個方程式左右都取模除 g （比較數學的講法是說同時投影至模除 g 的整數環）得到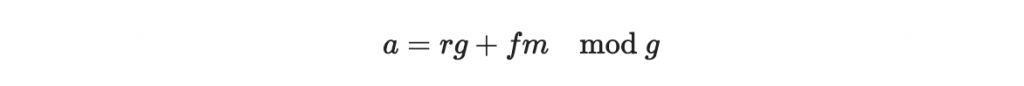

那其實根本就是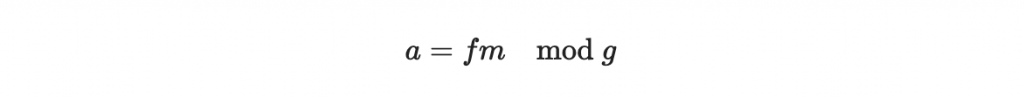

兩邊同時乘上 f 在模除 g 下的反元素：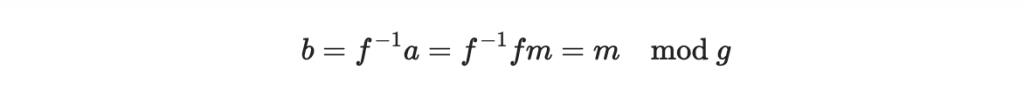

再次根據我們的構造條件：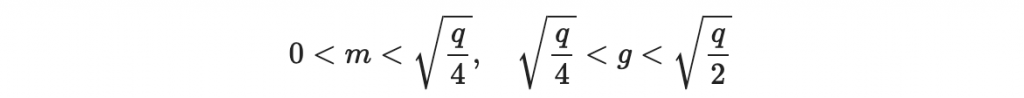

我們於是知道 m 根本就是一個小於 g 的數字，所以，跟剛剛一樣的理由，這裡的 b 也完完全全等於 m 。

晶格？

所以說好的晶格呢？😑
我們根本沒有用到什麼幾何的東西，哪來的晶格呢？？
這肯定是廣告不實！

明天我們就來看：「為什麼這是晶格密碼學？」

Takeaway

• 模除m的環中，若 a 的乘法反元素存在，記作 b ，則有 a * b mod m = 1.
• 模除m的環中，考慮數字 a ，當 a 與 m 最大公因數為 1 時，a 的乘法反元素存在，可以由擴展歐幾里德演算法來求得
• 在 SageMath 中，你可以用一行指令來求乘法反元素
• 一個你還沒看到晶格的晶格密碼系統（雖然是個簡單的系統，但是其中的證明技巧或論述還會在後面出現，算是一個伏筆）

ref

SILVERMAN, Joseph H.; PIPHER, Jill; HOFFSTEIN, Jeffrey. An introduction to mathematical cryptography. Springer New York, 2008.